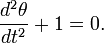Nonlinear system

From Wikipedia, the free encyclopedia

Jump to: navigation, search
 This article includes a list of references or external links, but its sources remain unclear because it has insufficient inline citations. Please help to improve this article by introducing more precise citations where appropriate. (March 2009)
This article describes the use of the term nonlinearity in mathematics. For other meanings, see nonlinearity (disambiguation).

In mathematics, a nonlinear system is a system which is not linear, that is, a system which does not satisfy the superposition principle, or whose output is not proportional to its input. Less technically, a nonlinear system is any problem where the variable(s) to be solved for cannot be written as a linear combination of independent components. A nonhomogeneous system, which is linear apart from the presence of a function of the independent variables, is nonlinear according to a strict definition, but such systems are usually studied alongside linear systems, because they can be transformed to a linear system of multiple variables.

Nonlinear problems are of interest to physicists and mathematicians because most physical systems are inherently nonlinear in nature. Nonlinear equations are difficult to solve and give rise to interesting phenomena such as chaos. The weather is famously nonlinear, where simple changes in one part of the system produce complex effects throughout.

Contents

[edit] Definition

In mathematics, a linear function (or map) f(x) is one which satisfies both of the following properties:

  • additivity, \textstyle f(x + y)\ = f(x)\ + f(y);
  • homogeneity, \textstyle f(\alpha x)\ = \alpha f(x).

(Additivity implies homogeneity for any rational α, and, for continuous functions, for any real α. For a complex α, homogeneity does not follow from additivity; for example, an antilinear map is additive but not homogeneous.)

An equation written as

f(x) = C\,

is called linear if f(x) is a linear map (as defined above) and nonlinear otherwise. The equation is called homogeneous if C = 0.

The definition f(x) = C is very general in that x can be any sensible mathematical object (number, vector, function, etc), and the function f(x) can literally be any mapping, including integration or differentiation with associated constraints (such as boundary values). If f(x) contains differentiation of x, the result will be a differential equation.

[edit] Nonlinear algebraic equations

Generally, nonlinear algebraic problems are often exactly solvable, and if not they usually can be thoroughly understood through qualitative and numeric analysis. As an example, the equation

x^2 + x - 1 = 0\,

may be written as

f(x) = C \quad \mbox{where} \quad f(x) = x^2 + x \quad \mbox{and} \quad C = 1\,

and is nonlinear because f(x) satisfies neither additivity nor homogeneity (the nonlinearity is due to the x2). Though nonlinear, this simple example may be solved exactly (via the quadratic formula) and is very well understood. On the other hand, the nonlinear equation

x^5 - x - 1 = 0\,

is not exactly solvable (see quintic equation), though it may be qualitatively analyzed and is well understood, for example through making a graph and examining the roots of f(x) − C = 0.

[edit] Nonlinear recurrence relations

A nonlinear recurrence relation defines successive terms of a sequence as a nonlinear function of preceding terms. Examples of nonlinear recurrence relations are the logistic map and the relations that define the various Hofstadter sequences.

[edit] Nonlinear differential equations

A system of differential equations is said to be nonlinear if it is not a linear system. Problems involving nonlinear differential equations are extremely diverse, and methods of solution or analysis are problem dependent. Examples of nonlinear differential equations are the Navier–Stokes equations in fluid dynamics, the Lotka–Volterra equations in biology, and the Black–Scholes PDE in finance.

One of the greatest difficulties of nonlinear problems is that it is not generally possible to combine known solutions into new solutions. In linear problems, for example, a family of linearly independent solutions can be used to construct general solutions through the superposition principle. A good example of this is one-dimensional heat transport with Dirichlet boundary conditions, the solution of which can be written as a time-dependent linear combination of sinusoids of differing frequencies; this makes solutions very flexible. It is often possible to find several very specific solutions to nonlinear equations, however the lack of a superposition principle prevents the construction of new solutions.

[edit] Ordinary differential equations

First order ordinary differential equations are often exactly solvable by separation of variables, especially for autonomous equations. For example, the nonlinear equation

\frac{\operatorname{d} u}{\operatorname{d} x} = -u^2\,

will easily yield u = (x + C) − 1 as a general solution which happens to be simpler than the solution to the linear equation \operatorname{d}u/\operatorname{d}x = -u. The equation is nonlinear because it may be written as

\frac{\operatorname{d} u}{\operatorname{d} x} + u^2=0\,

and the left-hand side of the equation is not a linear function of u and its derivatives. Note that if the u² term were replaced with u, the problem would be linear (the exponential decay problem).

Second and higher order ordinary differential equations (more generally, systems of nonlinear equations) rarely yield closed form solutions, though implicit solutions and solutions involving nonelementary integrals are encountered.

Common methods for the qualitative analysis of nonlinear ordinary differential equations include:

[edit] Partial differential equations

See also: List of nonlinear partial differential equations

The most common basic approach to studying nonlinear partial differential equations is to change the variables (or otherwise transform the problem) so that the resulting problem is simpler (possibly even linear). Sometimes, the equation may be transformed into one or more ordinary differential equations, as seen in the similarity transform or separation of variables, which is always useful whether or not the resulting ordinary differential equation(s) is solvable.

Another common (though less mathematic) tactic, often seen in fluid and heat mechanics, is to use scale analysis to simplify a general, natural equation in a certain specific boundary value problem. For example, the (very) nonlinear Navier-Stokes equations can be simplified into one linear partial differential equation in the case of transient, laminar, one dimensional flow in a circular pipe; the scale analysis provides conditions under which the flow is laminar and one dimensional and also yields the simplified equation.

Other methods include examining the characteristics and using the methods outlined above for ordinary differential equations.

[edit] Example: pendulum

Main article: Pendulum (mathematics)
Illustration of a pendulum.
Linearizations of a pendulum.

A classic, extensively studied nonlinear problem is the dynamics of a pendulum. Using Lagrangian mechanics, it may be shown[1] that the motion of a pendulum can be described by the dimensionless nonlinear equation

\frac{d^2 \theta}{d t^2} + \sin(\theta) = 0\,

where gravity is "down" and θ is as shown in the figure at right. One approach to "solving" this equation is to use dθ / dt as an integrating factor, which would eventually yield

\int \frac{d \theta}{\sqrt{C_0 + 2 \cos(\theta)}} = t + C_1\,

which is an implicit solution involving an elliptic integral. This "solution" generally does not have many uses because most of the nature of the solution is hidden in the nonelementary integral (nonelementary even if C0 = 0).

Another way to approach the problem is to linearize any nonlinearities (the sine function term in this case) at the various points of interest through Taylor expansions. For example, the linearization at θ = 0, called the small angle approximation, is

\frac{d^2 \theta}{d t^2} + \theta = 0\,

since \sin(\theta) \approx \theta for \theta \approx 0. This is a simple harmonic oscillator corresponding to oscillations of the pendulum near the bottom of its path. Another linearization would be at θ = π, corresponding to the pendulum being straight up:

\frac{d^2 \theta}{d t^2} + \pi - \theta = 0\,

since \sin(\theta) \approx \pi - \theta for \theta \approx \pi. The solution to this problem involves hyperbolic sinusoids, and note that unlike the small angle approximation, this approximation is unstable, meaning that | θ | will usually grow without limit, though bounded solutions are possible. This corresponds to the difficulty of balancing a pendulum upright, it is literally an unstable state.

One more interesting linearization is possible around θ = π / 2, around which \sin(\theta) \approx 1:

\frac{d^2 \theta}{d t^2} + 1 = 0.

This corresponds to a free fall problem. A very useful qualitative picture of the pendulum's dynamics may be obtained by piecing together such linearizations, as seen in the figure at right. Other techniques may be used to find (exact) phase portraits and approximate periods.

[edit] Metaphorical use

Engineers often use the term nonlinear to refer to irrational or erratic behavior, with the implication that the person who "goes nonlinear" is on the edge of losing control or even having a nervous breakdown.[2]

[edit] Types of nonlinear behaviors

  • Indeterminism - the behavior of a system cannot be predicted.
  • Multistability - alternating between two or more exclusive states.
  • Aperiodic oscillations - functions that do not repeat values after some period (otherwise known as chaotic oscillations or chaos).

[edit] Examples of nonlinear equations

See also the list of non-linear partial differential equations

[edit] See also

[edit] References

  1. ^ David Tong: Lectures on Classical Dynamics
  2. ^ Frank Rose (1990). West of Eden: The End of Innocence at Apple Computer. Frank Rose, publisher. ISBN 9780140093728. http://books.google.com/books?id=0DHnCxjX_t8C&pg=PA259&dq=go-nonlinear&lr=&as_brr=3&as_pt=ALLTYPES&ei=uJxJSfDvBouYMpOzwJAP. 

[edit] Further reading

[edit] External links

v • d • e
Systems and systems science
Systems categories
Systems
Theoretical fields
Systems scientists
Retrieved from "http://en.wikipedia.org/wiki/Nonlinear_system"
Personal tools