§10.22 Integrals
Contents
- §10.22(i) Indefinite Integrals
- §10.22(ii) Integrals over Finite Intervals
- §10.22(iii) Integrals over the Interval

- §10.22(iv) Integrals over the Interval

- §10.22(v) Hankel Transform
- §10.22(vi) Compendia
§10.22(i) Indefinite Integrals
In this subsection ![]() and
and ![]() denote
cylinder functions(§10.2(ii)) of orders
denote
cylinder functions(§10.2(ii)) of orders ![]() and
and ![]() ,
respectively, not necessarily distinct.
,
respectively, not necessarily distinct.
For the Struve function ![]() see §11.2(i).
see §11.2(i).
¶ Products
§10.22(ii) Integrals over Finite Intervals
Throughout this subsection ![]() .
.
¶ Trigonometric Arguments



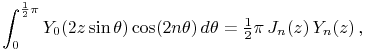




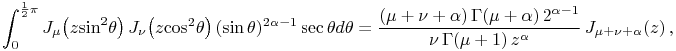
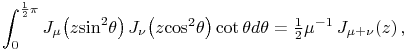
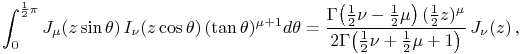
For ![]() see §10.25(ii).
see §10.25(ii).

¶ Products


¶ Convolutions

¶ Fractional Integral
§10.22(iii) Integrals over the Interval 
§10.22(iv) Integrals over the Interval 
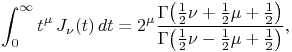

For ![]() see §10.25(ii).
see §10.25(ii).
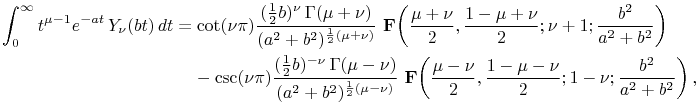
For the hypergeometric function ![]() see §15.2(i).
see §15.2(i).
For ![]() and
and ![]() see
§10.25(ii).
see
§10.25(ii).

For the confluent hypergeometric function ![]() see §13.2(i).
see §13.2(i).
¶ Orthogonality
¶ Weber–Schafheitlin Discontinuous Integrals, including Special Cases

If ![]() , then interchange
, then interchange ![]() and
and ![]() , and also
, and also ![]() and
and ![]() . If
. If ![]() ,
then
,
then

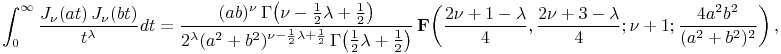
When ![]()


When ![]() ,
,

When ![]() ,
,

When ![]() ,
,
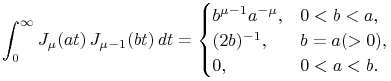
When ![]() and
and ![]() ,
,

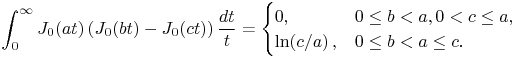
¶ Other Double Products
In (10.22.66)–(10.22.70) ![]() are positive
constants.
are positive
constants.
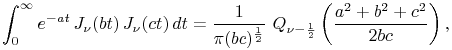
For the associated Legendre function ![]() see §14.3(ii)
with
see §14.3(ii)
with ![]() . For
. For ![]() and
and ![]() see §10.25(ii).
see §10.25(ii).
![\int _{0}^{\infty}\mathop{J_{{\nu}}\/}\nolimits\!\left(at\right)\mathop{J_{{\nu}}\/}\nolimits\!\left(bt\right)\frac{tdt}{t^{2}-z^{2}}=\left\{\begin{array}[]{ll}\frac{1}{2}\pi i\mathop{J_{{\nu}}\/}\nolimits\!\left(bz\right)\mathop{{H^{{(1)}}_{{\nu}}}\/}\nolimits\!\left(az\right),&a>b\\
\frac{1}{2}\pi i\mathop{J_{{\nu}}\/}\nolimits\!\left(az\right)\mathop{{H^{{(1)}}_{{\nu}}}\/}\nolimits\!\left(bz\right),&b>a\end{array}\right\},](https://webarchive.library.unt.edu/web/20130303070854im_/http://dlmf.nist.gov/10/22/E69.png)
Equation (10.22.70) also remains valid if the order ![]() of the
of the
![]() functions on both sides is replaced by
functions on both sides is replaced by ![]() ,
, ![]() ,
and the constraint
,
and the constraint ![]() is replaced by
is replaced by
![]() .
.
See also §1.17(ii) for an integral representation of the Dirac delta in terms of a product of Bessel functions.
¶ Triple Products
In (10.22.71) and (10.22.72) ![]() are positive
constants.
are positive
constants.


For the Ferrers function ![]() and the associated Legendre function
and the associated Legendre function ![]() , see
§§14.3(i) and 14.3(ii), respectively.
, see
§§14.3(i) and 14.3(ii), respectively.
In (10.22.74) and (10.22.75), ![]() are positive
constants and
are positive
constants and
(Thus if ![]() are the sides of a triangle, then
are the sides of a triangle, then ![]() is the
area of the triangle.)
is the
area of the triangle.)
If ![]() , then
, then

If ![]() , then
, then

§10.22(v) Hankel Transform
The Hankel transform (or Bessel transform) of a function
![]() is defined as
is defined as
§10.22(vi) Compendia
For collections of integrals of the functions ![]() ,
,
![]() ,
, ![]() , and
, and ![]() ,
including integrals with respect to the order, see
Andrews et al. (1999, pp. 216–225), Apelblat (1983, §12),
Erdélyi et al. (1953b, §§7.7.1–7.7.7 and 7.14–7.14.2),
Erdélyi et al. (1954a, b),
Gradshteyn and Ryzhik (2000, §§5.5 and 6.5–6.7),
Gröbner and Hofreiter (1950, pp. 196–204), Luke (1962),
Magnus et al. (1966, §3.8), Marichev (1983, pp. 191–216),
Oberhettinger (1974, §§1.10 and 2.7),
Oberhettinger (1990, §§1.13–1.16 and 2.13–2.16),
Oberhettinger and Badii (1973, §§1.14 and 2.12),
Okui (1974, 1975), Prudnikov et al. (1986b, §§1.8–1.10, 2.12–2.14,
3.2.4–3.2.7, 3.3.2, and 3.4.1),
Prudnikov et al. (1992a, §§3.12–3.14),
Prudnikov et al. (1992b, §§3.12–3.14),
Watson (1944, Chapters 5, 12, 13, and 14), and
Wheelon (1968).
,
including integrals with respect to the order, see
Andrews et al. (1999, pp. 216–225), Apelblat (1983, §12),
Erdélyi et al. (1953b, §§7.7.1–7.7.7 and 7.14–7.14.2),
Erdélyi et al. (1954a, b),
Gradshteyn and Ryzhik (2000, §§5.5 and 6.5–6.7),
Gröbner and Hofreiter (1950, pp. 196–204), Luke (1962),
Magnus et al. (1966, §3.8), Marichev (1983, pp. 191–216),
Oberhettinger (1974, §§1.10 and 2.7),
Oberhettinger (1990, §§1.13–1.16 and 2.13–2.16),
Oberhettinger and Badii (1973, §§1.14 and 2.12),
Okui (1974, 1975), Prudnikov et al. (1986b, §§1.8–1.10, 2.12–2.14,
3.2.4–3.2.7, 3.3.2, and 3.4.1),
Prudnikov et al. (1992a, §§3.12–3.14),
Prudnikov et al. (1992b, §§3.12–3.14),
Watson (1944, Chapters 5, 12, 13, and 14), and
Wheelon (1968).










