§14.28 Sums
Contents
§14.28(i) Addition Theorem
When ![]() ,
, ![]() ,
, ![]() , and
, and
![]() ,
,
14.28.1

where the branches of the square roots have their principal values when
![]() and are continuous when
and are continuous when
![]() . For this and similar results see
Erdélyi et al. (1953a, §3.11).
. For this and similar results see
Erdélyi et al. (1953a, §3.11).
§14.28(ii) Heine’s Formula
14.28.2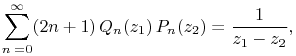
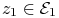 ,
,  ,
,
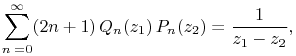
where ![]() and
and ![]() are ellipses with foci at
are ellipses with foci at ![]() ,
,
![]() being properly interior to
being properly interior to ![]() . The series
converges uniformly for
. The series
converges uniformly for ![]() outside or on
outside or on ![]() , and
, and ![]() within
or on
within
or on ![]() .
.
§14.28(iii) Other Sums
See §14.18(iv).

