§9.6 Relations to Other Functions
Contents
- §9.6(i) Airy Functions as Bessel Functions, Hankel Functions, and Modified Bessel Functions
- §9.6(ii) Bessel Functions, Hankel Functions, and Modified Bessel Functions as Airy Functions
- §9.6(iii) Airy Functions as Confluent Hypergeometric Functions
§9.6(i) Airy Functions as Bessel Functions, Hankel Functions, and Modified Bessel Functions
- Notes:
- These formulas are derivable from those given in Miller (1946, p. B17) and Olver (1997b, pp. 392–393).
- Keywords:
- Airy functions, Bessel functions, Hankel functions, modified Bessel functions
- Referenced by:
- ¶ ‣ §10.16, ¶ ‣ §10.39, ¶ ‣ §10.72(i), §9.17(iv)
- Permalink:
- http://dlmf.nist.gov/9.6.i
For the notation see §§10.2(ii) and 10.25(ii). With
9.6.1
- Symbols:
-
 : complex variable and
: complex variable and  : change of variable
: change of variable
- Referenced by:
- §9.6(iii), §9.6(iii), §9.7(iv)
- Permalink:
- http://dlmf.nist.gov/9.6.E1
- Encodings:
- TeX, pMML, png
9.6.2

- Symbols:
-
 : Airy function,
: Airy function,  : Bessel function of the third kind (or Hankel function),
: Bessel function of the third kind (or Hankel function),  : Bessel function of the third kind (or Hankel function),
: Bessel function of the third kind (or Hankel function),  : base of exponential function,
: base of exponential function, 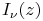 : modified Bessel function,
: modified Bessel function,  : modified Bessel function,
: modified Bessel function,  : complex variable and
: complex variable and  : change of variable
: change of variable
- A&S Ref:
- 10.4.14 (partial)
- Referenced by:
- §9.5(ii)
- Permalink:
- http://dlmf.nist.gov/9.6.E2
- Encodings:
- TeX, pMML, png
9.6.3

- Symbols:
-
 : Airy function,
: Airy function,  : Bessel function of the third kind (or Hankel function),
: Bessel function of the third kind (or Hankel function),  : Bessel function of the third kind (or Hankel function),
: Bessel function of the third kind (or Hankel function),  : base of exponential function,
: base of exponential function, 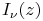 : modified Bessel function,
: modified Bessel function,  : modified Bessel function,
: modified Bessel function,  : complex variable and
: complex variable and  : change of variable
: change of variable
- A&S Ref:
- 10.4.16 (with opposite sign!)
- Permalink:
- http://dlmf.nist.gov/9.6.E3
- Encodings:
- TeX, pMML, png
9.6.4

- Symbols:
-
 : Airy function,
: Airy function,  : Bessel function of the third kind (or Hankel function),
: Bessel function of the third kind (or Hankel function),  : Bessel function of the third kind (or Hankel function),
: Bessel function of the third kind (or Hankel function),  : base of exponential function,
: base of exponential function, 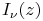 : modified Bessel function,
: modified Bessel function,  : complex variable and
: complex variable and  : change of variable
: change of variable
- A&S Ref:
- 10.4.18 (partial)
- Permalink:
- http://dlmf.nist.gov/9.6.E4
- Encodings:
- TeX, pMML, png
9.6.5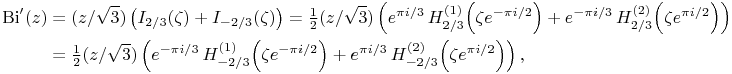
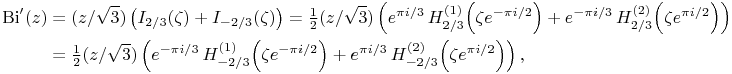
- Symbols:
-
 : Airy function,
: Airy function,  : Bessel function of the third kind (or Hankel function),
: Bessel function of the third kind (or Hankel function),  : Bessel function of the third kind (or Hankel function),
: Bessel function of the third kind (or Hankel function),  : base of exponential function,
: base of exponential function, 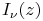 : modified Bessel function,
: modified Bessel function,  : complex variable and
: complex variable and  : change of variable
: change of variable
- A&S Ref:
- 10.4.20 (partial)
- Referenced by:
- §9.6(iii), §9.7(iv)
- Permalink:
- http://dlmf.nist.gov/9.6.E5
- Encodings:
- TeX, pMML, png
9.6.6

- Symbols:
-
 : Airy function,
: Airy function,  : Bessel function of the first kind,
: Bessel function of the first kind,  : Bessel function of the third kind (or Hankel function),
: Bessel function of the third kind (or Hankel function),  : Bessel function of the third kind (or Hankel function),
: Bessel function of the third kind (or Hankel function),  : base of exponential function,
: base of exponential function,  : complex variable and
: complex variable and  : change of variable
: change of variable
- A&S Ref:
- 10.4.15 (partial)
- Permalink:
- http://dlmf.nist.gov/9.6.E6
- Encodings:
- TeX, pMML, png
9.6.7

- Symbols:
-
 : Airy function,
: Airy function,  : Bessel function of the first kind,
: Bessel function of the first kind,  : Bessel function of the third kind (or Hankel function),
: Bessel function of the third kind (or Hankel function),  : Bessel function of the third kind (or Hankel function),
: Bessel function of the third kind (or Hankel function),  : base of exponential function,
: base of exponential function,  : complex variable and
: complex variable and  : change of variable
: change of variable
- A&S Ref:
- 10.4.17 (partial)
- Permalink:
- http://dlmf.nist.gov/9.6.E7
- Encodings:
- TeX, pMML, png
9.6.8

- Symbols:
-
 : Airy function,
: Airy function,  : Bessel function of the first kind,
: Bessel function of the first kind,  : Bessel function of the third kind (or Hankel function),
: Bessel function of the third kind (or Hankel function),  : Bessel function of the third kind (or Hankel function),
: Bessel function of the third kind (or Hankel function),  : base of exponential function,
: base of exponential function,  : complex variable and
: complex variable and  : change of variable
: change of variable
- A&S Ref:
- 10.4.19 (in slightly different form)
- Permalink:
- http://dlmf.nist.gov/9.6.E8
- Encodings:
- TeX, pMML, png
9.6.9

- Symbols:
-
 : Airy function,
: Airy function,  : Bessel function of the first kind,
: Bessel function of the first kind,  : Bessel function of the third kind (or Hankel function),
: Bessel function of the third kind (or Hankel function),  : Bessel function of the third kind (or Hankel function),
: Bessel function of the third kind (or Hankel function),  : base of exponential function,
: base of exponential function,  : complex variable and
: complex variable and  : change of variable
: change of variable
- A&S Ref:
- 10.4.21 (partial)
- Permalink:
- http://dlmf.nist.gov/9.6.E9
- Encodings:
- TeX, pMML, png
§9.6(ii) Bessel Functions, Hankel Functions, and Modified Bessel Functions as Airy Functions
- Notes:
- These formulas are derivable from those given in Olver (1997b, pp. 392–393).
- Keywords:
- Airy functions, Bessel functions, Hankel functions, modified Bessel functions
- Referenced by:
- ¶ ‣ §10.16, ¶ ‣ §10.39
- Permalink:
- http://dlmf.nist.gov/9.6.ii
Again, for the notation see §§10.2(ii) and 10.25(ii). With
9.6.10
- Symbols:
-
 : complex variable and
: complex variable and  : change of variable
: change of variable
- Permalink:
- http://dlmf.nist.gov/9.6.E10
- Encodings:
- TeX, pMML, png
9.6.11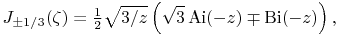
- Symbols:
-
 : Airy function,
: Airy function,  : Airy function,
: Airy function,  : Bessel function of the first kind,
: Bessel function of the first kind,  : complex variable and
: complex variable and  : change of variable
: change of variable
- A&S Ref:
- 10.4.22
- Permalink:
- http://dlmf.nist.gov/9.6.E11
- Encodings:
- TeX, pMML, png
9.6.12
- Symbols:
-
 : Airy function,
: Airy function,  : Airy function,
: Airy function,  : Bessel function of the first kind,
: Bessel function of the first kind,  : complex variable and
: complex variable and  : change of variable
: change of variable
- A&S Ref:
- 10.4.27
- Permalink:
- http://dlmf.nist.gov/9.6.E12
- Encodings:
- TeX, pMML, png
9.6.13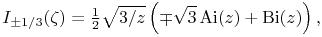
- Symbols:
-
 : Airy function,
: Airy function,  : Airy function,
: Airy function, 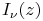 : modified Bessel function,
: modified Bessel function,  : complex variable and
: complex variable and  : change of variable
: change of variable
- A&S Ref:
- 10.4.25
- Permalink:
- http://dlmf.nist.gov/9.6.E13
- Encodings:
- TeX, pMML, png
9.6.14
- Symbols:
-
 : Airy function,
: Airy function,  : Airy function,
: Airy function, 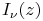 : modified Bessel function,
: modified Bessel function,  : complex variable and
: complex variable and  : change of variable
: change of variable
- A&S Ref:
- 10.4.30
- Permalink:
- http://dlmf.nist.gov/9.6.E14
- Encodings:
- TeX, pMML, png
9.6.15
- Symbols:
-
 : Airy function,
: Airy function,  : modified Bessel function,
: modified Bessel function,  : complex variable and
: complex variable and  : change of variable
: change of variable
- A&S Ref:
- 10.4.26
- Permalink:
- http://dlmf.nist.gov/9.6.E15
- Encodings:
- TeX, pMML, png
9.6.16
- Symbols:
-
 : Airy function,
: Airy function,  : modified Bessel function,
: modified Bessel function,  : complex variable and
: complex variable and  : change of variable
: change of variable
- A&S Ref:
- 10.4.31
- Permalink:
- http://dlmf.nist.gov/9.6.E16
- Encodings:
- TeX, pMML, png
9.6.17
- Symbols:
-
 : Airy function,
: Airy function,  : Airy function,
: Airy function,  : Bessel function of the third kind (or Hankel function),
: Bessel function of the third kind (or Hankel function),  : base of exponential function,
: base of exponential function,  : complex variable and
: complex variable and  : change of variable
: change of variable
- A&S Ref:
- 10.4.23 (with different sign, different form!)
- Referenced by:
- §9.8(i)
- Permalink:
- http://dlmf.nist.gov/9.6.E17
- Encodings:
- TeX, pMML, png
9.6.18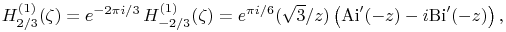
- Symbols:
-
 : Airy function,
: Airy function,  : Airy function,
: Airy function,  : Bessel function of the third kind (or Hankel function),
: Bessel function of the third kind (or Hankel function),  : base of exponential function,
: base of exponential function,  : complex variable and
: complex variable and  : change of variable
: change of variable
- A&S Ref:
- 10.4.28
- Referenced by:
- §9.8(i)
- Permalink:
- http://dlmf.nist.gov/9.6.E18
- Encodings:
- TeX, pMML, png
9.6.19
- Symbols:
-
 : Airy function,
: Airy function,  : Airy function,
: Airy function,  : Bessel function of the third kind (or Hankel function),
: Bessel function of the third kind (or Hankel function),  : base of exponential function,
: base of exponential function,  : complex variable and
: complex variable and  : change of variable
: change of variable
- A&S Ref:
- 10.4.24
- Permalink:
- http://dlmf.nist.gov/9.6.E19
- Encodings:
- TeX, pMML, png
9.6.20
- Symbols:
-
 : Airy function,
: Airy function,  : Airy function,
: Airy function,  : Bessel function of the third kind (or Hankel function),
: Bessel function of the third kind (or Hankel function),  : base of exponential function,
: base of exponential function,  : complex variable and
: complex variable and  : change of variable
: change of variable
- A&S Ref:
- 10.4.29
- Permalink:
- http://dlmf.nist.gov/9.6.E20
- Encodings:
- TeX, pMML, png
§9.6(iii) Airy Functions as Confluent Hypergeometric Functions
- Notes:
- For (9.6.21)–(9.6.24) combine (9.6.1)–(9.6.5) and (10.39.8)–(10.39.10). For (9.6.25), (9.6.26) combine (9.6.23), (9.6.24) with (13.14.2) and refer to §13.1.
- Keywords:
- Airy functions, confluent hypergeometric functions
- Permalink:
- http://dlmf.nist.gov/9.6.iii
For the notation see §§13.1, 13.2, and 13.14(i).
With ![]() as in (9.6.1),
as in (9.6.1),
9.6.21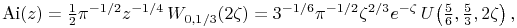
- Symbols:
-
 : Airy function,
: Airy function,  : Kummer confluent hypergeometric function,
: Kummer confluent hypergeometric function, 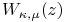 : Whittaker confluent hypergeometric function,
: Whittaker confluent hypergeometric function,  : base of exponential function,
: base of exponential function,  : complex variable and
: complex variable and  : change of variable
: change of variable
- Referenced by:
- §9.6(iii)
- Permalink:
- http://dlmf.nist.gov/9.6.E21
- Encodings:
- TeX, pMML, png
9.6.22
9.6.23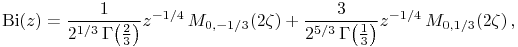
- Symbols:
-
 : Airy function,
: Airy function,  : gamma function,
: gamma function,  : Whittaker confluent hypergeometric function,
: Whittaker confluent hypergeometric function,  : complex variable and
: complex variable and  : change of variable
: change of variable
- Referenced by:
- §9.6(iii)
- Permalink:
- http://dlmf.nist.gov/9.6.E23
- Encodings:
- TeX, pMML, png
9.6.24

- Symbols:
-
 : Airy function,
: Airy function,  : gamma function,
: gamma function,  : Whittaker confluent hypergeometric function,
: Whittaker confluent hypergeometric function,  : complex variable and
: complex variable and  : change of variable
: change of variable
- Referenced by:
- §9.6(iii)
- Permalink:
- http://dlmf.nist.gov/9.6.E24
- Encodings:
- TeX, pMML, png
9.6.25

- Symbols:
-
 : Airy function,
: Airy function,  : gamma function,
: gamma function,  : generalized hypergeometric function,
: generalized hypergeometric function,  : base of exponential function,
: base of exponential function,  : complex variable and
: complex variable and  : change of variable
: change of variable
- Referenced by:
- §9.6(iii)
- Permalink:
- http://dlmf.nist.gov/9.6.E25
- Encodings:
- TeX, pMML, png
9.6.26

- Symbols:
-
 : Airy function,
: Airy function,  : gamma function,
: gamma function,  : generalized hypergeometric function,
: generalized hypergeometric function,  : base of exponential function,
: base of exponential function,  : complex variable and
: complex variable and  : change of variable
: change of variable
- Referenced by:
- §9.6(iii)
- Permalink:
- http://dlmf.nist.gov/9.6.E26
- Encodings:
- TeX, pMML, png

