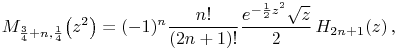§13.18 Relations to Other Functions
Contents
- §13.18(i) Elementary Functions
- §13.18(ii) Incomplete Gamma Functions
- §13.18(iii) Modified Bessel Functions
- §13.18(iv) Parabolic Cylinder Functions
- §13.18(v) Orthogonal Polynomials
§13.18(i) Elementary Functions
13.18.1
13.18.2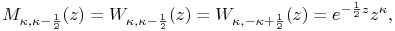
13.18.3
§13.18(ii) Incomplete Gamma Functions
§13.18(iii) Modified Bessel Functions
§13.18(iv) Parabolic Cylinder Functions
For the notation see §12.2.
13.18.11
13.18.12
13.18.13