§14.30 Spherical and Spheroidal Harmonics

Keywords:: Ferrers functions, spherical harmonics, spheroidal harmonics
Referenced by:: ¶ ‣ §1.17(iii), ¶ ‣ §18.38(ii), §34.3(vii)
Permalink:: http://dlmf.nist.gov/14.30

§14.30(i) Definitions
§14.30(ii) Basic Properties
§14.30(iii) Sums
§14.30(iv) Applications

§14.30(i) Definitions

Notes:: See Edmonds (1974, p. 24).
Keywords:: sectorial harmonics, spherical harmonics, spheroidal harmonics, surface harmonics of the first kind, tesseral harmonics
Referenced by:: §10.73(ii)
Permalink:: http://dlmf.nist.gov/14.30.i

With $l$ and $m$ integers such that $0\leq m\leq l$ , and $\theta$ and $\phi$ angles such that $0\leq\theta\leq\pi$ , $0\leq\phi\leq 2\pi$ ,

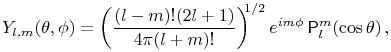
14.30.1 $\mathop{Y_{{{l},{m}}}\/}\nolimits\!\left(\theta,\phi\right)=\left(\frac{(l-m)!(2l+1)}{4\pi(l+m)!}\right)^{{1/2}}e^{{im\phi}}\mathop{\mathsf{P}^{{m}}_{{l}}\/}\nolimits\!\left(\mathop{\cos\/}\nolimits\theta\right),$

Defines:: $\mathop{Y_{{{l},{m}}}\/}\nolimits\!\left(\theta,\phi\right)$ : spherical harmonic
Symbols:: $\mathop{\mathsf{P}^{{\mu}}_{{\nu}}\/}\nolimits\!\left(x\right)$ : Ferrers function of the first kind, $\mathop{\cos\/}\nolimits z$ : cosine function, $e$ : base of exponential function, $!$ : $n!$ : factorial, $m$ : nonnegative integer and $l$ : nonnegative integer
Referenced by:: §14.30(i), §14.30(ii), §14.30(ii), §14.30(iv)
Permalink:: http://dlmf.nist.gov/14.30.E1
Encodings:: TeX, pMML, png

14.30.2 $\mathop{Y_{{l}}^{{m}}\/}\nolimits\!\left(\theta,\phi\right)=\mathop{\cos\/}\nolimits\!\left(m\phi\right)\mathop{\mathsf{P}^{{m}}_{{l}}\/}\nolimits\!\left(\mathop{\cos\/}\nolimits\theta\right)\text{ or }\mathop{\sin\/}\nolimits\!\left(m\phi\right)\mathop{\mathsf{P}^{{m}}_{{l}}\/}\nolimits\!\left(\mathop{\cos\/}\nolimits\theta\right).$

Defines:: $\mathop{Y_{{l}}^{{m}}\/}\nolimits\!\left(\theta,\phi\right)$ : surface harmonic of the first kind
Symbols:: $\mathop{\mathsf{P}^{{\mu}}_{{\nu}}\/}\nolimits\!\left(x\right)$ : Ferrers function of the first kind, $\mathop{\cos\/}\nolimits z$ : cosine function, $\mathop{\sin\/}\nolimits z$ : sine function, $m$ : nonnegative integer and $l$ : nonnegative integer
Permalink:: http://dlmf.nist.gov/14.30.E2
Encodings:: TeX, pMML, png

$\mathop{Y_{{{l},{m}}}\/}\nolimits\!\left(\theta,\phi\right)$ are known as spherical harmonics. $\mathop{Y_{{l}}^{{m}}\/}\nolimits\!\left(\theta,\phi\right)$ are known as surface harmonics of the first kind: tesseral for $m<l$ and sectorial for $m=l$ . Sometimes $\mathop{Y_{{{l},{m}}}\/}\nolimits\!\left(\theta,\phi\right)$ is denoted by $i^{{-l}}\mathfrak{D}_{{lm}}(\theta,\phi)$ ; also the definition of $\mathop{Y_{{{l},{m}}}\/}\nolimits\!\left(\theta,\phi\right)$ can differ from (14.30.1), for example, by inclusion of a factor $(-1)^{m}$ .

$\mathop{P^{{m}}_{{n}}\/}\nolimits\!\left(x\right)$ and $\mathop{Q^{{m}}_{{n}}\/}\nolimits\!\left(x\right)$ ( $x>1$ ) are often referred to as the prolate spheroidal harmonics of the first and second kinds, respectively. $\mathop{P^{{m}}_{{n}}\/}\nolimits\!\left(ix\right)$ and $\mathop{Q^{{m}}_{{n}}\/}\nolimits\!\left(ix\right)$ ( $x>0$ ) are known as oblate spheroidal harmonics of the first and second kinds, respectively. Segura and Gil (1999) introduced the scaled oblate spheroidal harmonics $R_{n}^{m}(x)=e^{{-i\pi n/2}}\mathop{P^{{m}}_{{n}}\/}\nolimits\!\left(ix\right)$ and $T_{n}^{m}(x)=ie^{{i\pi n/2}}\mathop{Q^{{m}}_{{n}}\/}\nolimits\!\left(ix\right)$ which are real when $x>0$ and $n=0,1,2,\dots$ .

§14.30(ii) Basic Properties

Notes:: For (14.30.3), (14.30.6), and (14.30.8) see Edmonds (1974, pp. 20–21). (Note that Edmonds’ $P_{l}^{m}(x)$ differs by a factor $(-1)^{m}$ from $\mathop{\mathsf{P}^{{m}}_{{l}}\/}\nolimits\!\left(x\right)$ .) (14.30.4) may be derived from (14.8.1), (14.8.2), and (14.30.1). (14.30.5) may be derived from (14.5.1) and (14.30.1). (14.30.7) may be derived from (14.7.17) and (14.30.1). (14.30.3) also follows from (14.30.1) and (14.7.10).
Keywords:: spherical harmonics
Permalink:: http://dlmf.nist.gov/14.30.ii

Most mathematical properties of $\mathop{Y_{{{l},{m}}}\/}\nolimits\!\left(\theta,\phi\right)$ can be derived directly from (14.30.1) and the properties of the Ferrers function of the first kind given earlier in this chapter.

¶ Explicit Representation

14.30.3 $\mathop{Y_{{{l},{m}}}\/}\nolimits\!\left(\theta,\phi\right)=\frac{(-1)^{{l+m}}}{2^{l}l!}\left(\frac{(l-m)!(2l+1)}{4\pi(l+m)!}\right)^{{1/2}}e^{{im\phi}}\left(\mathop{\sin\/}\nolimits\theta\right)^{m}\*\left(\frac{d}{d(\mathop{\cos\/}\nolimits\theta)}\right)^{{l+m}}\left(\mathop{\sin\/}\nolimits\theta\right)^{{2l}}.$

Symbols:: $\mathop{\cos\/}\nolimits z$ : cosine function, $\frac{df}{dx}$ : derivative of $f$ with respect to $x$ , $e$ : base of exponential function, $!$ : $n!$ : factorial, $\mathop{\sin\/}\nolimits z$ : sine function, $\mathop{Y_{{{l},{m}}}\/}\nolimits\!\left(\theta,\phi\right)$ : spherical harmonic, $m$ : nonnegative integer and $l$ : nonnegative integer
Referenced by:: §14.30(ii)
Permalink:: http://dlmf.nist.gov/14.30.E3
Encodings:: TeX, pMML, png

¶ Special Values

14.30.4 $\mathop{Y_{{{l},{m}}}\/}\nolimits\!\left(0,\phi\right)=\begin{cases}\left(\dfrac{2l+1}{4\pi}\right)^{{1/2}},&m=0,\\ 0,&m=1,2,3,\dots,\end{cases}$

Symbols:: $\mathop{Y_{{{l},{m}}}\/}\nolimits\!\left(\theta,\phi\right)$ : spherical harmonic, $m$ : nonnegative integer and $l$ : nonnegative integer
Referenced by:: §14.30(ii)
Permalink:: http://dlmf.nist.gov/14.30.E4
Encodings:: TeX, pMML, png

14.30.5 $\mathop{Y_{{{l},{m}}}\/}\nolimits\!\left(\tfrac{1}{2}\pi,\phi\right)=\begin{cases}\dfrac{(-1)^{{(l+m)/2}}e^{{im\phi}}}{2^{l}\left(\frac{1}{2}l-\frac{1}{2}m\right)!\left(\frac{1}{2}l+\frac{1}{2}m\right)!}\left(\dfrac{(l-m)!(l+m)!(2l+1)}{4\pi}\right)^{{1/2}},&\frac{1}{2}l+\frac{1}{2}m\in\Integer,\\ 0,&\frac{1}{2}l+\frac{1}{2}m\notin\Integer.\end{cases}$

Symbols:: $\in$ : element of, $e$ : base of exponential function, $!$ : $n!$ : factorial, $\Integer$ : set of all integers, $\notin$ : not an element of, $\mathop{Y_{{{l},{m}}}\/}\nolimits\!\left(\theta,\phi\right)$ : spherical harmonic, $m$ : nonnegative integer and $l$ : nonnegative integer
Referenced by:: §14.30(ii)
Permalink:: http://dlmf.nist.gov/14.30.E5
Encodings:: TeX, pMML, png

¶ Symmetry

14.30.6 $\mathop{Y_{{{l},{-m}}}\/}\nolimits\!\left(\theta,\phi\right)=(-1)^{m}{\mathop{Y_{{{l},{m}}}\/}\nolimits^{{*}}}\!\left(\theta,\phi\right).$

Symbols:: $\mathop{Y_{{{l},{m}}}\/}\nolimits\!\left(\theta,\phi\right)$ : spherical harmonic, $m$ : nonnegative integer and $l$ : nonnegative integer
Referenced by:: §14.30(ii)
Permalink:: http://dlmf.nist.gov/14.30.E6
Encodings:: TeX, pMML, png

¶ Parity Operation

14.30.7 $\mathop{Y_{{{l},{m}}}\/}\nolimits\!\left(\pi-\theta,\phi+\pi\right)=(-1)^{l}\mathop{Y_{{{l},{m}}}\/}\nolimits\!\left(\theta,\phi\right).$

Symbols:: $\mathop{Y_{{{l},{m}}}\/}\nolimits\!\left(\theta,\phi\right)$ : spherical harmonic, $m$ : nonnegative integer and $l$ : nonnegative integer
Referenced by:: §14.30(ii)
Permalink:: http://dlmf.nist.gov/14.30.E7
Encodings:: TeX, pMML, png

¶ Orthogonality

Keywords:: spherical harmonics

14.30.8 $\int _{{0}}^{{2\pi}}\!\!\int _{{0}}^{{\pi}}{\mathop{Y_{{{l_{1}},{m_{1}}}}\/}\nolimits^{{*}}}\!\left(\theta,\phi\right)\mathop{Y_{{{l_{2}},{m_{2}}}}\/}\nolimits\!\left(\theta,\phi\right)\mathop{\sin\/}\nolimits\theta d\theta d\phi=\delta _{{l_{1},l_{2}}}\delta _{{m_{1},m_{2}}};$

Symbols:: $\delta _{{j,k}}$ : Kronecker delta, $dx$ : differential of $x$ , $\int$ : integral, $\mathop{\sin\/}\nolimits z$ : sine function, $\mathop{Y_{{{l},{m}}}\/}\nolimits\!\left(\theta,\phi\right)$ : spherical harmonic, $m$ : nonnegative integer and $l$ : nonnegative integer
Referenced by:: §14.30(ii)
Permalink:: http://dlmf.nist.gov/14.30.E8
Encodings:: TeX, pMML, png

here and elsewhere in this section the asterisk (*) denotes complex conjugate.

See also (34.3.22), and for further related integrals see Askey et al. (1986).

§14.30(iii) Sums

Notes:: See Edmonds (1974, p. 63).
Keywords:: spherical harmonics
Permalink:: http://dlmf.nist.gov/14.30.iii

¶ Distributional Completeness

Keywords:: spherical harmonics

For a series representation of the product of two Dirac deltas in terms of products of spherical harmonics see §1.17(iii).

¶ Addition Theorem

Keywords:: spherical harmonics

14.30.9 $\mathop{\mathsf{P}_{{l}}\/}\nolimits\!\left(\mathop{\cos\/}\nolimits\theta _{1}\mathop{\cos\/}\nolimits\theta _{2}+\mathop{\sin\/}\nolimits\theta _{1}\mathop{\sin\/}\nolimits\theta _{2}\mathop{\cos\/}\nolimits\!\left(\phi _{1}-\phi _{2}\right)\right)=\frac{4\pi}{2l+1}\sum _{{m=-l}}^{{l}}{\mathop{Y_{{{l},{m}}}\/}\nolimits^{{*}}}\!\left(\theta _{1},\phi _{1}\right)\mathop{Y_{{{l},{m}}}\/}\nolimits\!\left(\theta _{2},\phi _{2}\right).$

Symbols:: $\mathop{\mathsf{P}^{{\mu}}_{{\nu}}\/}\nolimits\!\left(x\right)$ : Ferrers function of the first kind, $\mathop{\cos\/}\nolimits z$ : cosine function, $\mathop{\sin\/}\nolimits z$ : sine function, $\mathop{Y_{{{l},{m}}}\/}\nolimits\!\left(\theta,\phi\right)$ : spherical harmonic, $m$ : nonnegative integer and $l$ : nonnegative integer
Referenced by:: ¶ ‣ §18.18(ii)
Permalink:: http://dlmf.nist.gov/14.30.E9
Encodings:: TeX, pMML, png

§14.30(iv) Applications

Notes:: See Edmonds (1974, pp. 21–22).
Keywords:: Ferrers functions, Laplace’s equation, angular momentum operator, geophysics, homogeneous harmonic polynomials, reduced Planck’s constant, spherical coordinates, spherical harmonics
Referenced by:: ¶ ‣ §1.5(ii)
Permalink:: http://dlmf.nist.gov/14.30.iv

In general, spherical harmonics are defined as the class of homogeneous harmonic polynomials. See Andrews et al. (1999, Chapter 9). The special class of spherical harmonics $\mathop{Y_{{{l},{m}}}\/}\nolimits\!\left(\theta,\phi\right)$ , defined by (14.30.1), appear in many physical applications. As an example, Laplace’s equation $\nabla^{2}W=0$ in spherical coordinates (§1.5(ii)):

14.30.10 ${\frac{1}{\rho^{2}}\frac{\partial}{\partial\rho}\left(\rho^{2}\frac{\partial W}{\partial\rho}\right)+\frac{1}{\rho^{2}\mathop{\sin\/}\nolimits\theta}\frac{\partial}{\partial\theta}\left(\mathop{\sin\/}\nolimits\theta\frac{\partial W}{\partial\theta}\right)}+\frac{1}{\rho^{2}{\mathop{\sin\/}\nolimits^{{2}}}\theta}\frac{{\partial}^{2}W}{{\partial\phi}^{2}}=0,$

Symbols:: $\frac{\partial f}{\partial x}$ : partial derivative of $f$ with respect to $x$ , $\mathop{\sin\/}\nolimits z$ : sine function and $W(\rho,\theta,\phi)$ : solution
Permalink:: http://dlmf.nist.gov/14.30.E10
Encodings:: TeX, pMML, png

has solutions $W(\rho,\theta,\phi)=\rho^{l}\mathop{Y_{{{l},{m}}}\/}\nolimits\!\left(\theta,\phi\right)$ , which are everywhere one-valued and continuous.

In the quantization of angular momentum the spherical harmonics $\mathop{Y_{{{l},{m}}}\/}\nolimits\!\left(\theta,\phi\right)$ are normalized solutions of the eigenvalue equation

14.30.11 $\mathrm{L}^{2}\mathop{Y_{{{l},{m}}}\/}\nolimits=\hbar^{2}l(l+1)\mathop{Y_{{{l},{m}}}\/}\nolimits,$

Symbols:: $\mathop{Y_{{{l},{m}}}\/}\nolimits\!\left(\theta,\phi\right)$ : spherical harmonic, $m$ : nonnegative integer, $l$ : nonnegative integer and $\mathrm{L}$ : angular momentum operator
Permalink:: http://dlmf.nist.gov/14.30.E11
Encodings:: TeX, pMML, png

where $\hbar$ is the reduced Planck’s constant, and $\mathrm{L}^{2}$ is the angular momentum operator in spherical coordinates:

14.30.12 $\mathrm{L}^{2}=-\hbar^{2}\left(\frac{1}{\mathop{\sin\/}\nolimits\theta}\frac{\partial}{\partial\theta}\left(\mathop{\sin\/}\nolimits\theta\frac{\partial}{\partial\theta}\right)+\frac{1}{{\mathop{\sin\/}\nolimits^{{2}}}\theta}\frac{{\partial}^{2}}{{\partial\phi}^{2}}\right);$

Symbols:: $\frac{\partial f}{\partial x}$ : partial derivative of $f$ with respect to $x$ , $\mathop{\sin\/}\nolimits z$ : sine function and $\mathrm{L}$ : angular momentum operator
Permalink:: http://dlmf.nist.gov/14.30.E12
Encodings:: TeX, pMML, png

see Edmonds (1974, §2.5).

For applications in geophysics see Stacey (1977, §§4.2, 6.3, and 8.1).