§11.14 Tables

Permalink:: http://dlmf.nist.gov/11.14

§11.14(i) Introduction
§11.14(ii) Struve Functions
§11.14(iii) Integrals
§11.14(iv) Anger–Weber Functions
§11.14(v) Incomplete Functions

§11.14(i) Introduction

Permalink:: http://dlmf.nist.gov/11.14.i

For tables before 1961 see Fletcher et al. (1962) and Lebedev and Fedorova (1960). Tables listed in these Indices are omitted from the subsections that follow.

§11.14(ii) Struve Functions

Keywords:: Struve functions and modified Struve functions
Permalink:: http://dlmf.nist.gov/11.14.ii

Abramowitz and Stegun (1964, Chapter 12) tabulates $\mathop{\mathbf{H}_{{n}}\/}\nolimits\!\left(x\right)$ , $\mathop{\mathbf{H}_{{n}}\/}\nolimits\!\left(x\right)-\mathop{Y_{{n}}\/}\nolimits\!\left(x\right)$ , and $\mathop{I_{{n}}\/}\nolimits\!\left(x\right)-\mathop{\mathbf{L}_{{n}}\/}\nolimits\!\left(x\right)$ for $n=0,1$ and $x=0(.1)5$ , $x^{{-1}}=0(.01)0.2$ to 6D or 7D.
Agrest et al. (1982) tabulates $\mathop{\mathbf{H}_{{n}}\/}\nolimits\!\left(x\right)$ and $e^{{-x}}\mathop{\mathbf{L}_{{n}}\/}\nolimits\!\left(x\right)$ for $n=0,1$ and $x=0(.001)5(.005)15(.01)100$ to 11D.
Barrett (1964) tabulates $\mathop{\mathbf{L}_{{n}}\/}\nolimits\!\left(x\right)$ for $n=0,1$ and $x=0.2(.005)4(.05)10(.1)19.2$ to 5 or 6S, $x=6(.25)59.5(.5)100$ to 2S.
Zanovello (1975) tabulates $\mathop{\mathbf{H}_{{n}}\/}\nolimits\!\left(x\right)$ for $n=-4(1)15$ and $x=0.5(.5)26$ to 8D or 9S.
Zhang and Jin (1996) tabulates $\mathop{\mathbf{H}_{{n}}\/}\nolimits\!\left(x\right)$ and $\mathop{\mathbf{L}_{{n}}\/}\nolimits\!\left(x\right)$ for $n=-4(1)3$ and $x=0(1)20$ to 8D or 7S.

§11.14(iii) Integrals

Keywords:: Struve functions and modified Struve functions, integrals
Permalink:: http://dlmf.nist.gov/11.14.iii

Abramowitz and Stegun (1964, Chapter 12) tabulates $\int _{0}^{x}(\mathop{I_{{0}}\/}\nolimits\!\left(t\right)-\mathop{\mathbf{L}_{{0}}\/}\nolimits\!\left(t\right))dt$ and $(2/\pi)\int _{x}^{\infty}t^{{-1}}\mathop{\mathbf{H}_{{0}}\/}\nolimits\!\left(t\right)dt$ for $x=0(.1)5$ to 5D or 7D; $\int _{0}^{x}(\mathop{\mathbf{H}_{{0}}\/}\nolimits\!\left(t\right)-\mathop{Y_{{0}}\/}\nolimits\!\left(t\right))dt-(2/\pi)\mathop{\ln\/}\nolimits x$ , $\int _{0}^{x}(\mathop{I_{{0}}\/}\nolimits\!\left(t\right)-\mathop{\mathbf{L}_{{0}}\/}\nolimits\!\left(t\right))dt-(2/\pi)\mathop{\ln\/}\nolimits x$ , and $\int _{x}^{\infty}t^{{-1}}(\mathop{\mathbf{H}_{{0}}\/}\nolimits\!\left(t\right)-\mathop{Y_{{0}}\/}\nolimits\!\left(t\right))dt$ for $x^{{-1}}=0(.01)0.2$ to 6D.
Agrest et al. (1982) tabulates $\int _{0}^{x}\mathop{\mathbf{H}_{{0}}\/}\nolimits\!\left(t\right)dt$ and $e^{{-x}}\int _{0}^{x}\mathop{\mathbf{L}_{{0}}\/}\nolimits\!\left(t\right)dt$ for $x=0(.001)5(.005)15(.01)100$ to 11D.

§11.14(iv) Anger–Weber Functions

Keywords:: Anger–Weber functions
Permalink:: http://dlmf.nist.gov/11.14.iv

Bernard and Ishimaru (1962) tabulates $\mathop{\mathbf{J}_{{\nu}}\/}\nolimits\!\left(x\right)$ and $\mathop{\mathbf{E}_{{\nu}}\/}\nolimits\!\left(x\right)$ for $\nu=-10(.1)10$ and $x=0(.1)10$ to 5D.
Jahnke and Emde (1945) tabulates $\mathop{\mathbf{E}_{{n}}\/}\nolimits\!\left(x\right)$ for $n=1,2$ and $x=0(.01)14.99$ to 4D.

§11.14(v) Incomplete Functions

Keywords:: Anger–Weber functions, Struve functions and modified Struve functions
Permalink:: http://dlmf.nist.gov/11.14.v

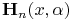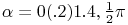Agrest and Maksimov (1971, Chapter 11) defines incomplete Struve, Anger, and Weber functions and includes tables of an incomplete Struve function $\mathop{\mathbf{H}_{{n}}\/}\nolimits\!\left(x,\alpha\right)$ for $n=0,1$ , $x=0(.2)10$ , and $\alpha=0(.2)1.4,\tfrac{1}{2}\pi$ , together with surface plots.

§11.14 Tables

Contents

§11.14(i) Introduction

§11.14(ii) Struve Functions

§11.14(iii) Integrals

§11.14(iv) Anger–Weber Functions

§11.14(v) Incomplete Functions