§19.5 Maclaurin and Related Expansions
If ![]() and
and ![]() , then
, then
19.5.1

where ![]() is the Gauss hypergeometric function
(§§15.1 and 15.2(i)).
is the Gauss hypergeometric function
(§§15.1 and 15.2(i)).
19.5.2

19.5.3

19.5.4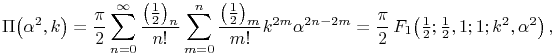
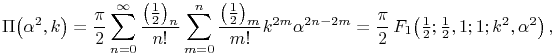
where ![]() is an Appell function
(§16.13).
is an Appell function
(§16.13).
For Jacobi’s nome ![]() :
:
19.5.5
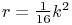 ,
, 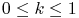 .
.
Also,
19.5.6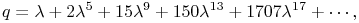
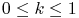 ,
,
where
19.5.7
Coefficients of terms up to ![]() are given in Lee (1990),
along with tables of fractional errors in
are given in Lee (1990),
along with tables of fractional errors in ![]() and
and
![]() ,
, ![]() , obtained by using 12 different truncations of
(19.5.6) in (19.5.8) and (19.5.9).
, obtained by using 12 different truncations of
(19.5.6) in (19.5.8) and (19.5.9).
19.5.8
 ,
,

19.5.9
 .
.

An infinite series for ![]() is equivalent to the infinite
product
is equivalent to the infinite
product
19.5.10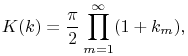
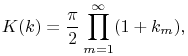
where ![]() and
and
19.5.11
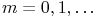 .
.


