§16.15 Integral Representations and Integrals
16.15.1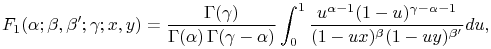
 ,
, 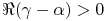 ,
,
16.15.2
 ,
,
 ,
,

16.15.3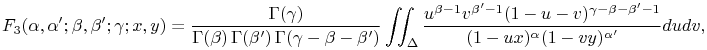
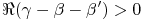 ,
,
 ,
,  ,
,
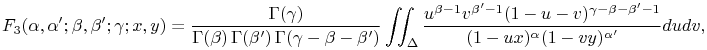
where ![]() is the triangle defined by
is the triangle defined by ![]() ,
, ![]() ,
, ![]() .
.
16.15.4
 ,
,
 .
.

For these and other formulas, including double Mellin–Barnes integrals, see
Erdélyi et al. (1953a, §5.8). These representations can be used to derive
analytic continuations of the Appell functions, including convergent series
expansions for large ![]() , large
, large ![]() , or both. For inverse Laplace transforms
of Appell functions see Prudnikov et al. (1992b, §3.40).
, or both. For inverse Laplace transforms
of Appell functions see Prudnikov et al. (1992b, §3.40).

