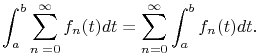§1.9 Calculus of a Complex Variable
Contents
- §1.9(i) Complex Numbers
- §1.9(ii) Continuity, Point Sets, and Differentiation
- §1.9(iii) Integration
- §1.9(iv) Conformal Mapping
- §1.9(v) Infinite Sequences and Series
- §1.9(vi) Power Series
- §1.9(vii) Inversion of Limits
§1.9(i) Complex Numbers
¶ Real and Imaginary Parts
¶ Polar Representation
where
and when ![]() ,
,
according as ![]() lies in the 1st, 2nd, 3rd, or 4th quadrants. Here
lies in the 1st, 2nd, 3rd, or 4th quadrants. Here
¶ Modulus and Phase
The principal value
of ![]() corresponds to
corresponds to ![]() , that is,
, that is, ![]() . It
is single-valued on
. It
is single-valued on ![]() , except on the interval
, except on the interval
![]() where it is discontinuous and two-valued. Unless indicated
otherwise, these principal values are assumed throughout
the DLMF. (However, if we
require a principal value to be single-valued, then we can restrict
where it is discontinuous and two-valued. Unless indicated
otherwise, these principal values are assumed throughout
the DLMF. (However, if we
require a principal value to be single-valued, then we can restrict
![]() .)
.)
where
see §4.14.
¶ Complex Conjugate
¶ Arithmetic Operations
¶ Powers
¶ DeMoivre’s Theorem
¶ Triangle Inequality
§1.9(ii) Continuity, Point Sets, and Differentiation
¶ Continuity
A function ![]() is continuous at a point
is continuous at a point ![]() if
if
![]() . That is, given any positive number
. That is, given any positive number
![]() , however small, we can find a positive number
, however small, we can find a positive number ![]() such that
such that
![]() for all
for all ![]() in the open disk
in the open disk ![]() .
.
¶ Point Sets in 
A neighborhood of a point ![]() is a disk
is a disk ![]() . An
open set in
. An
open set in ![]() is one in which each point has a neighborhood
that is contained in the set.
is one in which each point has a neighborhood
that is contained in the set.
A point ![]() is a limit point (limiting point or
accumulation point) of a set of points
is a limit point (limiting point or
accumulation point) of a set of points ![]() in
in ![]() (or
(or
![]() ) if every neighborhood of
) if every neighborhood of ![]() contains a point of
contains a point of ![]() distinct from
distinct from ![]() . (
. (![]() may or may not belong to
may or may not belong to ![]() .) As a consequence,
every neighborhood of a limit point of
.) As a consequence,
every neighborhood of a limit point of ![]() contains an infinite number of
points of
contains an infinite number of
points of ![]() .
Also, the union of
.
Also, the union of ![]() and its limit points is the closure of
and its limit points is the closure of ![]() .
.
A domain
![]() , say, is an open set in
, say, is an open set in ![]() that is connected,
that is, any two points can be joined by a polygonal arc (a finite chain of
straight-line segments) lying in the set. Any point whose neighborhoods always
contain members and nonmembers of
that is connected,
that is, any two points can be joined by a polygonal arc (a finite chain of
straight-line segments) lying in the set. Any point whose neighborhoods always
contain members and nonmembers of ![]() is a boundary point
of
is a boundary point
of ![]() . When its boundary points are added the domain is said to be
closed,
but unless specified otherwise a domain is assumed to be open.
. When its boundary points are added the domain is said to be
closed,
but unless specified otherwise a domain is assumed to be open.
A region is an open domain together with none, some, or all of its boundary points. Points of a region that are not boundary points are called interior points.
A function ![]() is continuous on a region
is continuous on a region ![]() if for each point
if for each point ![]() in
in ![]() and any given number
and any given number ![]() (
(![]() ) we can find a neighborhood of
) we can find a neighborhood of
![]() such that
such that ![]() for all points
for all points ![]() in the
intersection of the neighborhood with
in the
intersection of the neighborhood with ![]() .
.
¶ Differentiation
A function ![]() is differentiable at a point
is differentiable at a point ![]() if the following
limit exists:
if the following
limit exists:
Differentiability automatically implies continuity.
¶ Cauchy–Riemann Equations
If ![]() exists at
exists at ![]() and
and ![]() , then
, then
at ![]() .
.
Conversely, if at a given point ![]() the partial derivatives
the partial derivatives
![]() ,
, ![]() ,
, ![]() , and
, and ![]() exist, are continuous, and satisfy (1.9.25), then
exist, are continuous, and satisfy (1.9.25), then ![]() is
differentiable at
is
differentiable at ![]() .
.
¶ Analyticity
A function ![]() is said to be analytic (holomorphic) at
is said to be analytic (holomorphic) at
![]() if it is differentiable in a neighborhood of
if it is differentiable in a neighborhood of ![]() .
.
A function ![]() is analytic in a domain
is analytic in a domain
![]() if it is analytic at each point of
if it is analytic at each point of ![]() . A function analytic at every point
of
. A function analytic at every point
of ![]() is said to be entire.
is said to be entire.
If ![]() is analytic in an open domain
is analytic in an open domain ![]() , then each of its derivatives
, then each of its derivatives
![]() ,
, ![]() ,
, ![]() exists and is analytic in
exists and is analytic in ![]() .
.
¶ Harmonic Functions
If ![]() is analytic in an open domain
is analytic in an open domain ![]() , then
, then ![]() and
and
![]() are
harmonic in
are
harmonic in ![]() , that is,
, that is,
or in polar form ((1.9.3)) ![]() and
and ![]() satisfy
satisfy
at all points of ![]() .
.
§1.9(iii) Integration
An arc ![]() is given by
is given by ![]() ,
, ![]() , where
, where
![]() and
and ![]() are continuously differentiable. If
are continuously differentiable. If ![]() and
and ![]() are
continuous and
are
continuous and ![]() and
and ![]() are piecewise continuous, then
are piecewise continuous, then ![]() defines a contour.
defines a contour.
A contour is simple if it contains no multiple points, that is, for
every pair of distinct values ![]() of
of ![]() ,
, ![]() . A
simple closed contour is a simple contour, except that
. A
simple closed contour is a simple contour, except that ![]() .
.
Next,
for a contour ![]() and
and ![]() continuous,
continuous, ![]() . If
. If ![]() ,
, ![]() , then the integral is defined analogously to the
infinite integrals in §1.4(v). Similarly when
, then the integral is defined analogously to the
infinite integrals in §1.4(v). Similarly when ![]() or
or
![]() .
.
¶ Jordan Curve Theorem
Any simple closed contour ![]() divides
divides ![]() into two open domains that
have
into two open domains that
have ![]() as common boundary. One of these domains is bounded and is called the
interior domain of
as common boundary. One of these domains is bounded and is called the
interior domain of ![]() ; the other is unbounded and is called the
exterior domain of
; the other is unbounded and is called the
exterior domain of ![]() .
.
¶ Cauchy’s Theorem
If ![]() is continuous within and on a simple closed contour
is continuous within and on a simple closed contour ![]() and analytic
within
and analytic
within ![]() , then
, then
¶ Cauchy’s Integral Formula
If ![]() is continuous within and on a simple closed contour
is continuous within and on a simple closed contour ![]() and analytic
within
and analytic
within ![]() , and if
, and if ![]() is a point within
is a point within ![]() , then
, then
and
provided that in both cases ![]() is described in the positive rotational
(anticlockwise) sense.
is described in the positive rotational
(anticlockwise) sense.
¶ Liouville’s Theorem
Any bounded entire function is a constant.
¶ Winding Number
If ![]() is a closed contour, and
is a closed contour, and ![]() , then
, then
where ![]() is an integer called the winding number of
is an integer called the winding number of ![]() with respect to
with respect to ![]() . If
. If ![]() is simple and oriented in the positive
rotational sense, then
is simple and oriented in the positive
rotational sense, then ![]() is 1 or 0 depending whether
is 1 or 0 depending whether
![]() is inside or outside
is inside or outside ![]() .
.
¶ Mean Value Property
For ![]() harmonic,
harmonic,
¶ Poisson Integral
If ![]() is continuous on
is continuous on ![]() , then with
, then with ![]()
is harmonic in ![]() . Also with
. Also with ![]() ,
,
![]() as
as ![]() within
within ![]() .
.
§1.9(iv) Conformal Mapping
The extended complex plane,
![]() , consists of the points of the complex plane
, consists of the points of the complex plane
![]() together with an ideal point
together with an ideal point ![]() called the point at
infinity.
A system of open disks around infinity is given by
called the point at
infinity.
A system of open disks around infinity is given by
Each ![]() is a neighborhood
of
is a neighborhood
of ![]() . Also,
. Also,
A function ![]() is analytic at
is analytic at ![]() if
if ![]() is analytic
at
is analytic
at ![]() , and we set
, and we set ![]() .
.
¶ Conformal Transformation
Suppose ![]() is analytic in a domain
is analytic in a domain ![]() and
and ![]() are two arcs in
are two arcs in ![]() passing through
passing through ![]() . Let
. Let ![]() be the images of
be the images of ![]() and
and ![]() under
the mapping
under
the mapping ![]() . The angle between
. The angle between ![]() and
and ![]() at
at
![]() is the angle between the tangents to the two arcs at
is the angle between the tangents to the two arcs at ![]() , that is, the
difference of the signed angles that the tangents make with the positive
direction of the real axis. If
, that is, the
difference of the signed angles that the tangents make with the positive
direction of the real axis. If ![]() , then the angle between
, then the angle between ![]() and
and ![]() equals the angle between
equals the angle between ![]() and
and ![]() both in magnitude and
sense. We then say that the mapping
both in magnitude and
sense. We then say that the mapping ![]() is conformal
(angle-preserving) at
is conformal
(angle-preserving) at ![]() .
.
The linear transformation ![]() ,
, ![]() , has
, has ![]() and
and ![]() maps
maps ![]() conformally onto
conformally onto ![]() .
.
¶ Bilinear Transformation
The transformation (1.9.40) is a one-to-one conformal mapping
of ![]() onto itself.
onto itself.
The cross ratio
of ![]() is defined by
is defined by
or its limiting form, and is invariant under bilinear transformations.
Other names for the bilinear transformation are fractional linear transformation, homographic transformation, and Möbius transformation.
§1.9(v) Infinite Sequences and Series
A sequence ![]() converges
to
converges
to ![]() if
if ![]() . For
. For ![]() , the
sequence
, the
sequence ![]() converges iff the sequences
converges iff the sequences ![]() and
and ![]() separately converge. A series
separately converge. A series ![]() converges
if the sequence
converges
if the sequence ![]() converges. The series is
divergent if
converges. The series is
divergent if ![]() does not converge. The series converges
absolutely if
does not converge. The series converges
absolutely if ![]() converges. A series
converges. A series
![]() converges (diverges) absolutely when
converges (diverges) absolutely when
![]() (
(![]() ), or when
), or when
![]() (
(![]() ).
Absolutely convergent series are also convergent.
).
Absolutely convergent series are also convergent.
Let ![]() be a sequence of functions defined on a set
be a sequence of functions defined on a set ![]() . This
sequence converges pointwise
to a function
. This
sequence converges pointwise
to a function ![]() if
if
for each ![]() . The sequence converges uniformly
on
. The sequence converges uniformly
on ![]() , if for every
, if for every ![]() there exists an integer
there exists an integer ![]() , independent of
, independent of
![]() , such that
, such that
for all ![]() and
and ![]() .
.
A series
![]() converges uniformly on
converges uniformly on ![]() , if the sequence
, if the sequence
![]() converges uniformly on
converges uniformly on ![]() .
.
¶ Weierstrass 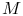 -test
-test
Suppose ![]() is a sequence of real numbers such that
is a sequence of real numbers such that
![]() converges and
converges and ![]() for all
for all ![]() and all
and all ![]() . Then the series
. Then the series ![]() converges
uniformly on
converges
uniformly on ![]() .
.
A doubly-infinite series
![]() converges (uniformly) on
converges (uniformly) on ![]() iff each of the
series
iff each of the
series ![]() and
and ![]() converges
(uniformly) on
converges
(uniformly) on ![]() .
.
§1.9(vi) Power Series
For a series ![]() there is a number
there is a number ![]() ,
, ![]() , such that the series converges for all
, such that the series converges for all ![]() in
in ![]() and
diverges for
and
diverges for ![]() in
in ![]() . The circle
. The circle ![]() is called the
circle of convergence
of the series, and
is called the
circle of convergence
of the series, and ![]() is the radius of convergence. Inside the circle
the sum of the series is an analytic function
is the radius of convergence. Inside the circle
the sum of the series is an analytic function ![]() . For
. For ![]() in
in
![]() (
(![]() ), the convergence is absolute and
uniform. Moreover,
), the convergence is absolute and
uniform. Moreover,
and
For the converse of this result see §1.10(i).
¶ Operations
When ![]() and
and ![]() both converge
both converge
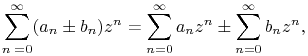
and

where

Next, let
Then the expansions (1.9.54), (1.9.57), and
(1.9.60) hold for all sufficiently small ![]() .
.
where
With ![]() ,
,
(principal value), where
and
Also,
(principal value), where ![]() ,
,
and
For the definitions of the principal values of ![]() and
and ![]() see §§4.2(i) and 4.2(iv).
see §§4.2(i) and 4.2(iv).
Lastly, a power series can be differentiated any number of times within its circle of convergence:
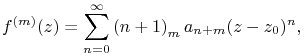
§1.9(vii) Inversion of Limits
¶ Double Sequences and Series
A set of complex numbers ![]() where
where ![]() and
and ![]() take all positive
integer values is called a double sequence. It converges to
take all positive
integer values is called a double sequence. It converges to ![]() if for every
if for every ![]() , there is an integer
, there is an integer ![]() such that
such that
for all ![]() . Suppose
. Suppose ![]() converges to
converges to ![]() and the repeated
limits
and the repeated
limits
exist. Then both repeated limits equal ![]() .
.
A double series is the limit of the double sequence
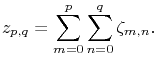
If the limit exists, then the double series is convergent; otherwise it
is divergent. The double series is absolutely convergent if it is
convergent when ![]() is replaced by
is replaced by ![]() .
.
If a double series is absolutely convergent, then it is also convergent and its sum is given by either of the repeated sums
¶ Term-by-Term Integration
Suppose the series ![]() , where
, where ![]() is continuous,
converges uniformly on every compact set
of a domain
is continuous,
converges uniformly on every compact set
of a domain ![]() , that is, every closed and bounded set in
, that is, every closed and bounded set in ![]() . Then
. Then

for any finite contour ![]() in
in ![]() .
.
¶ Dominated Convergence Theorem
Let ![]() be a finite or infinite interval, and
be a finite or infinite interval, and ![]() be real or complex continuous functions,
be real or complex continuous functions, ![]() . Suppose
. Suppose
![]() converges uniformly in any compact interval in
converges uniformly in any compact interval in
![]() , and at least one of the following two conditions is satisfied:
, and at least one of the following two conditions is satisfied:
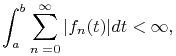
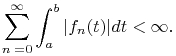
Then